I was recently reading an article in "A Gardner's Workout - Training the Mind and Entertaining the Spirit" by Martin Gardner.
Title: Covering the cube with congruent polygons", Page 73.
The problem is about cutting the cubical "surface" into a tiling made of a specific number (n) of congruent polygons. And examining if any cases are impossible ...
n=2,3 etc are simple(he states - and the tiles are basically rectangles.
He also gives an example of a very "esoteric" tiling using Latin crosses as tiles. This is wonderful - I have no idea how someone could have come up with that solution. (Unfortunately, I don't have the drawing skills are patience to draw a picture of that solution here. May be one of these days ...)
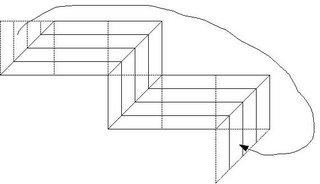
He challenged his readers to give a solution for n=7, that is tile using 7 congruent polygonal tiles. And he was astonished that "Anneke Treep" came up with not one solution, but four solutions each of which solves the problem for any number of polygonal tiles (Ignoring limitations imposed by structure of matter , of course). I have depicted one of those solutions below.
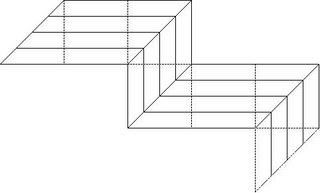
I was thinking of the process by which this solution could be obtained. And here is one possibility.
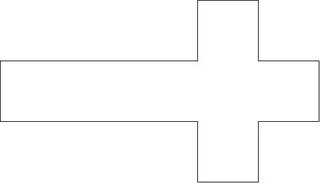
The key insight is that the cube needs to be unwrapped(development of surfaces) such that there are no branches in the resulting planar development.I shall not rigorously define branching here, but intuitive definition will do: if you draw the mid line of the strip it does not branch as a Y anywhere. Of course its tautological. You know what I mean, c'mon. Its not like the picture below. So there.
Now that allows us to draw "parallels" inside the development and divide the figure into any number of polygonal pieces. So lets start with the following attempt.
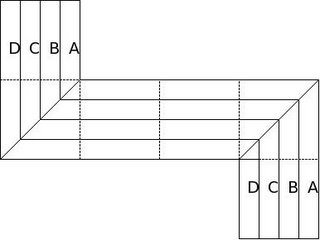
The problem with the above solution is obvious - the polygonal pieces A, B, C and D are not congruent - this is because of the varying lengths - sides becoming longer as we progress towards D. This is because of a sloping diagonal and the non-sloping edge. If the edge was also sloping, it would allows us to retain the same length of the "arm" and hence obtain a solution. So lets move a piece of triangle from the top square to the bottom square. Like so:
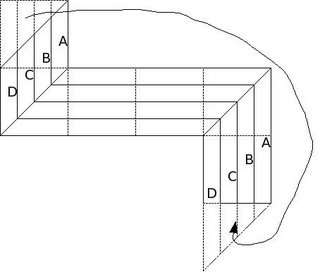
Now, this seems like a plausible solution. But wait a second! the two squares are actually "lids" for opposite faces of a cube. Therefore, If a cube was brought to life from a piece paper that looks like above, it would be cancerous. One big triangular hole on one face and a triangular Growth" on the opposite face.
What this tells us is that, if the face from which we cut and and the face to which paste are adjacent this solution works. And so we obtain this:
Puzzles







